Propensity Score Matching

library(tidyverse)
library(flextable)
library(TH.data)
library(gtsummary)
library(MatchIt)
library(cobalt)
library(ggrepel)
library(officer) # for fp_border

1. Dataset Overview

Description

A data frame containing the observations from the GBSG2 study (n=686).

Variables

horTh: hormonal therapy, a factor at two levels no and yes.
age: age of the patients in years.
menostat: menopausal status, a factor at two levels pre (premenopausal) and post (postmenopausal).
tsize: tumor size (in mm).
tgrade: tumor grade, a ordered factor at levels I < II < III.
pnodes: number of positive nodes.
progrec: progesterone receptor (in fmol).
estrec: estrogen receptor (in fmol).
time: recurrence free survival time (in days).
cens: censoring indicator (0- censored, 1- event).

Source

W. Sauerbrei and P. Royston (1999). Building multivariable prognostic and diagnostic models: transformation of the predictors by using fractional polynomials. Journal of the Royal Statistics Society Series A, Volume 162(1), 71–94.

2. Summary Table

Following is a summary table of the data set. There were significant difference in the age (P<0.001), menostat (P<0.001), and estrec (P=0.009) variables between hormone therapy treatments(no vs. yes).

GBSG2[,1:8] %>% tbl_summary(by=horTh) %>% add_overall() %>% add_p() %>% 
    separate_p_footnotes()

Characteristic	Overall, N = 686¹	no, N = 440¹	yes, N = 246¹	p-value
age	53 (46, 61)	50 (45, 59)	58 (50, 63)	<0.001²
menostat				<0.001³
Pre	290 (42%)	231 (52%)	59 (24%)
Post	396 (58%)	209 (48%)	187 (76%)
tsize	25 (20, 35)	25 (20, 35)	25 (20, 35)	0.5²
tgrade				0.3³
I	81 (12%)	48 (11%)	33 (13%)
II	444 (65%)	281 (64%)	163 (66%)
III	161 (23%)	111 (25%)	50 (20%)
pnodes	3 (1, 7)	3 (1, 7)	3 (1, 7)	0.4²
progrec	32 (7, 132)	32 (7, 130)	35 (7, 133)	0.6²
estrec	36 (8, 114)	32 (8, 92)	46 (9, 182)	0.009²
¹ Median (IQR); n (%)
² Wilcoxon rank sum test
³ Pearson's Chi-squared test

3. Matching using Nearest Neighbor

Following is the result of 1:1 nearest neighbor matching without replacement

matched <- matchit(formula = horTh ~ age + menostat + tsize + tgrade + pnodes + progrec + estrec, data = GBSG2)
matched

## A matchit object
##  - method: 1:1 nearest neighbor matching without replacement
##  - distance: Propensity score
##              - estimated with logistic regression
##  - number of obs.: 686 (original), 492 (matched)
##  - target estimand: ATT
##  - covariates: age, menostat, tsize, tgrade, pnodes, progrec, estrec

summary(matched)

## 
## Call:
## matchit(formula = horTh ~ age + menostat + tsize + tgrade + pnodes + 
##     progrec + estrec, data = GBSG2)
## 
## Summary of Balance for All Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
## distance            0.4157        0.3267          0.6761     0.8882    0.1738
## age                56.6220       51.0568          0.5911     0.8931    0.1025
## menostatPre         0.2398        0.5250         -0.6679          .    0.2852
## menostatPost        0.7602        0.4750          0.6679          .    0.2852
## tsize              28.8049       29.6227         -0.0579     0.9614    0.0177
## tgradeI             0.1341        0.1091          0.0735          .    0.0251
## tgradeII            0.6626        0.6386          0.0507          .    0.0240
## tgradeIII           0.2033        0.2523         -0.1218          .    0.0490
## pnodes              5.1301        4.9432          0.0350     0.9209    0.0102
## progrec           124.2927      102.0023          0.0893     2.1571    0.0177
## estrec            125.8171       79.7227          0.2412     2.3660    0.0762
##              eCDF Max
## distance       0.3272
## age            0.2738
## menostatPre    0.2852
## menostatPost   0.2852
## tsize          0.0450
## tgradeI        0.0251
## tgradeII       0.0240
## tgradeIII      0.0490
## pnodes         0.0539
## progrec        0.0496
## estrec         0.1417
## 
## 
## Summary of Balance for Matched Data:
##              Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
## distance            0.4157        0.4105          0.0398     1.1060    0.0083
## age                56.6220       56.2398          0.0406     1.0584    0.0119
## menostatPre         0.2398        0.2439         -0.0095          .    0.0041
## menostatPost        0.7602        0.7561          0.0095          .    0.0041
## tsize              28.8049       29.1545         -0.0248     1.0651    0.0120
## tgradeI             0.1341        0.1179          0.0477          .    0.0163
## tgradeII            0.6626        0.6829         -0.0430          .    0.0203
## tgradeIII           0.2033        0.1992          0.0101          .    0.0041
## pnodes              5.1301        5.3943         -0.0495     0.7438    0.0108
## progrec           124.2927      117.0447          0.0290     1.6818    0.0120
## estrec            125.8171      112.6667          0.0688     1.5573    0.0165
##              eCDF Max Std. Pair Dist.
## distance       0.0366          0.0428
## age            0.0447          0.5700
## menostatPre    0.0041          0.0095
## menostatPost   0.0041          0.0095
## tsize          0.0407          0.9500
## tgradeI        0.0163          0.5487
## tgradeII       0.0203          0.8683
## tgradeIII      0.0041          0.7374
## pnodes         0.0407          0.9519
## progrec        0.0488          0.5928
## estrec         0.0528          0.5584
## 
## Sample Sizes:
##           Control Treated
## All           440     246
## Matched       246     246
## Unmatched     194       0
## Discarded       0       0

4. Matched Data (n=492)

Following is first 6 rows of the matched data.

data <- match.data(matched)

head(data)  %>%
    flextable() %>%
    autofit()

horTh	age	menostat	tsize	tgrade	pnodes	progrec	estrec	time	cens	distance	weights	subclass
no	70	Post	21	II	3	48	66	1,814	1	0.5203676	1	120
yes	56	Post	12	II	7	61	77	2,018	1	0.4563422	1	36
yes	58	Post	35	II	9	52	271	712	1	0.4939083	1	84
yes	59	Post	17	II	4	60	29	1,807	1	0.4562091	1	118
no	73	Post	35	II	1	26	65	772	1	0.5253295	1	83
yes	59	Post	8	II	2	181	0	2,172	0	0.4561443	1	240

5. Covariates vs. Propensity Score

Following is visual inspection of whether matching is done well using a loess smoother to estimate the mean of each covariate, by treatment status, at each value of the propensity score.

plot1 <- data %>%
    mutate(across(!horTh,as.numeric)) %>%
    pivot_longer(cols = age:progrec, names_to = "variable", values_to = "response") %>%
    ggplot(aes(x = distance, y = response, color = as.factor(horTh))) +
    geom_point(alpha = 0.2, size = 1.3) +
    geom_smooth(method = "loess", se = F) +
    labs(x="Propensity score", y="", color = "horTh")+
    theme_bw() +
    facet_wrap(vars(variable), scales = "free", ncol = 2)

plot1

6. Change of Absolute Standardized Differences

Following is a visualization of difference in absolute standardized differences of covariates between all data and matched data.

ChASD <- function(x, show.table = TRUE, xpos = NULL, ypos = NULL) {
    res = summary(x)$sum.all[, 3]
    if (is.null(summary(x)$sum.matched)) {
        res2 = summary(x)$sum.across[, 3]
    } else {
        res2 = summary(x)$sum.matched[, 3]
    }
    # res
    # res2
    df1 = data.frame(value = abs(res))
    df1$name = "All Data"
    df2 = data.frame(value = abs(res2))
    df2$name = "Matched Data"
    df = rbind(df1, df2)
    rownames(df1)
    df$var = rep(rownames(df1), 2)
    # df
    df3 = cbind(abs(res), abs(res2))
    colnames(df3) = c("All Data", "Matched")
    # df3
    df3 = df3[order(df3[, 1], decreasing = TRUE), ]
    if (is.null(ypos)) {
        maxy = max(res)
        miny = max(res2)
        ypos = miny + (maxy - miny) * 1/2
    }
    if (is.null(xpos))
        xpos = 1.5
    table_grob = gridExtra::tableGrob(round(df3, 3), theme = gridExtra::ttheme_minimal())
    p <- ggplot(data = df, aes_string(x = "name", y = "value", color = "var", group = "var",
        label = "var")) + 
        geom_point() + geom_line() + 
        xlab("") + ylab("Absolute Standardized Diff in Means") +
        guides(colour = "none") + 
        ggrepel::geom_text_repel(data = df[df$name == "All Data",], hjust = 1.2) + 
        ggrepel::geom_text_repel(data = df[df$name != "All Data",], hjust = -0.2) + 
        theme_bw()
    if (show.table)
        p <- p + annotation_custom(grob = table_grob, xmin = xpos, ymin = ypos)
    p
}

# methods(class="matchit")
# ?plot.summary.matchit
# ?summary.matchit
ChASD(matched)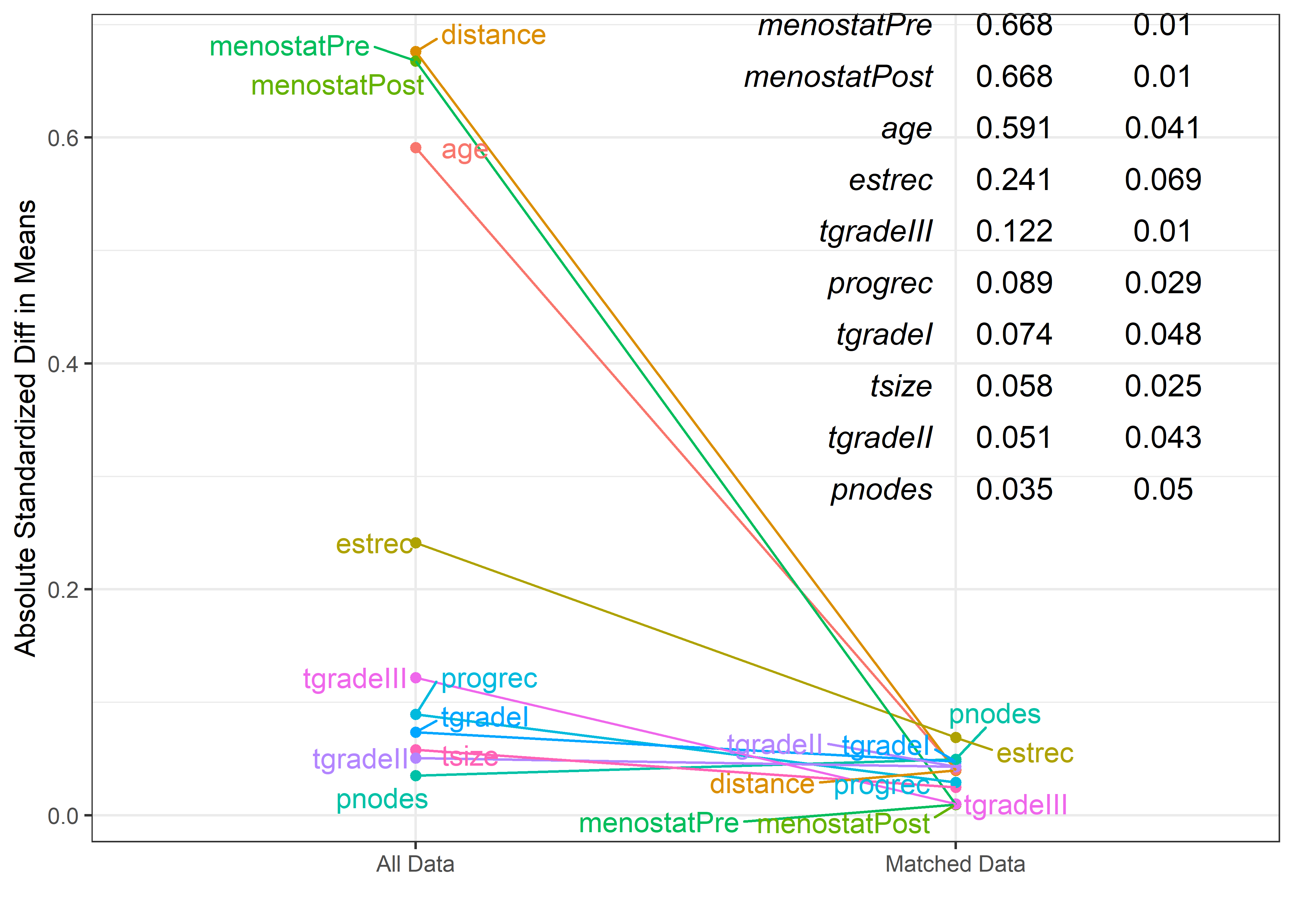

7. Distribution of Propensity Score

Following is a visualization of distribution of propensity scores (distance) of those who were matched.

plot(matched, type = "jitter", col = "blue", interactive = FALSE)

8. Histogram of Propensity Score

Following is a visualization of distribution of propensity scores (distance) before and after matching.

plot(matched, type = "hist", interactive = FALSE)

9. Balance Table

Following is a table of balance statistics computed before matching and those computed after matching.

bal.tab(matched, un = TRUE, stats = c("m", "v"))

## Call
##  matchit(formula = horTh ~ age + menostat + tsize + tgrade + pnodes + 
##     progrec + estrec, data = GBSG2)
## 
## Balance Measures
##                   Type Diff.Un V.Ratio.Un Diff.Adj V.Ratio.Adj
## distance      Distance  0.6761     0.8882   0.0398      1.1060
## age            Contin.  0.5911     0.8931   0.0406      1.0584
## menostat_Post   Binary  0.2852          .   0.0041           .
## tsize          Contin. -0.0579     0.9614  -0.0248      1.0651
## tgrade_I        Binary  0.0251          .   0.0163           .
## tgrade_II       Binary  0.0240          .  -0.0203           .
## tgrade_III      Binary -0.0490          .   0.0041           .
## pnodes         Contin.  0.0350     0.9209  -0.0495      0.7438
## progrec        Contin.  0.0893     2.1571   0.0290      1.6818
## estrec         Contin.  0.2412     2.3660   0.0688      1.5573
## 
## Sample sizes
##           Control Treated
## All           440     246
## Matched       246     246
## Unmatched     194       0

10. Love Plot

Following are love plots of chosen balance statistics (standardized mean differences and variance ratios)

10-1. Standardized mean differences

love.plot(matched, stats="mean.diffs", binary="std", 
          var.order="unadjusted", grid=TRUE, thresholds=0.1,
          sample.names= c("Unmatched", "Matched"))

10-2. Variance ratios

love.plot(matched, stats = "variance.ratios", 
          var.order = "unadjusted", grid=TRUE, thresholds=1, 
          sample.names= c("Unmatched", "Matched"))

11. Mirror Plot

Following is a visualization of distributional balance for distance.

bal.plot(matched, var.name = "distance", mirror = TRUE, type = "histogram", which = "both")

12. Before and after propensity score matching

Following is a summary table of the data before matching and after matching.

aa <- GBSG2[,1:8] %>% tbl_summary(by=horTh) %>% add_overall() %>% add_p() %>%
    as_tibble()

names(aa) <- c("Variable", paste0(names(aa[-1]),"_Before Mathcing")) %>%
    str_remove_all("\\*\\*")


bb <- data[,1:8] %>% tbl_summary(by=horTh) %>% add_overall() %>% add_p() %>%
    as_tibble()

names(bb) <- c("Variable", paste0(names(bb[-1]),"_After Matching")) %>%
    str_remove_all("\\*\\*")

cc <- aa %>%
    left_join(bb, by="Variable") 


headers <-  list(tibble(col_keys = colnames(cc)) %>%
    separate(
      col = col_keys,
      into = c("line1", "line2"),
      sep = "_",
      remove = FALSE,
      fill = "right"
    ) %>%
    relocate(line2, .before = line1)
  )

big_border = fp_border(color="black", width = 2)

vv<- cc %>%
    flextable(col_keys = names(.))   %>%
    set_header_df(mapping = headers, key = "col_keys") %>% 
    merge_h(part = "header") %>%
    theme_vanilla() %>%
    # theme_booktabs(bold_header = TRUE) %>%
    # vline(j=c(1,5), border = big_border) %>%
    # valign(j = c("Variable"), valign = "center") %>%
    align(align = "center", part = "header") %>%
    align(j = c(2:9), align = "right", part = "body") %>%
    fontsize(size = 8, part = "body") %>%
    add_footer_row(values = "Median (IQR); n (%)", colwidths = 9) %>%
    vline(j=c(1,5), border = NULL, part = "all") %>%
    hline_bottom(border = big_border, part = "footer") %>%
    fix_border_issues() %>%
    autofit()

vv

	Before Mathcing	After Matching
age	53 (46, 61)	50 (45, 59)	58 (50, 63)	<0.001	58 (50, 63)	58 (50, 63)	58 (50, 63)	0.7
menostat				<0.001				>0.9
Pre	290 (42%)	231 (52%)	59 (24%)		119 (24%)	60 (24%)	59 (24%)
Post	396 (58%)	209 (48%)	187 (76%)		373 (76%)	186 (76%)	187 (76%)
tsize	25 (20, 35)	25 (20, 35)	25 (20, 35)	0.5	25 (20, 35)	25 (20, 35)	25 (20, 35)	0.8
tgrade				0.3				0.8
I	81 (12%)	48 (11%)	33 (13%)		62 (13%)	29 (12%)	33 (13%)
II	444 (65%)	281 (64%)	163 (66%)		331 (67%)	168 (68%)	163 (66%)
III	161 (23%)	111 (25%)	50 (20%)		99 (20%)	49 (20%)	50 (20%)
pnodes	3 (1, 7)	3 (1, 7)	3 (1, 7)	0.4	3 (1, 7)	3 (2, 7)	3 (1, 7)	>0.9
progrec	32 (7, 132)	32 (7, 130)	35 (7, 133)	0.6	40 (7, 142)	41 (7, 147)	35 (7, 133)	0.7
estrec	36 (8, 114)	32 (8, 92)	46 (9, 182)	0.009	50 (10, 162)	52 (10, 152)	46 (9, 182)	>0.9
Median (IQR); n (%)

13. Summary of Propensity Score Matching

We used propensity score matching to estimate the average marginal effect of the horTh on cens on those who received it accounting for confounding by the included covariates. We first attempted 1:1 nearest neighbor propensity score matching without replacement with a propensity score estimated using logistic regression of the treatment on the covariates. 1:1 nearest matching on the propensity score without replacement, which yielded adequate balance, as indicated in tables and figures. After matching, all standardized mean differences for the covariates were below 0.1 and all standardized mean differences for squares and two-way interactions between covariates were below 0.15, indicating adequate balance. The propensity score was estimated using a logistic regression of the horTh on the covariates.